坐标转换

发表于 2022/03/14 更新于 2024/08/23

作者

11 分钟阅读

坐标转换

坐标转换

本文主要介绍ECEF（地心地固坐标）、LLA（经纬高；WGS-84坐标）、ENU（站心坐标；东北天坐标）。

坐标转换

GNSS全称是全球导航卫星系统（Global Navigation Satellite System）

1 坐标分类

1.1 ECEF坐标

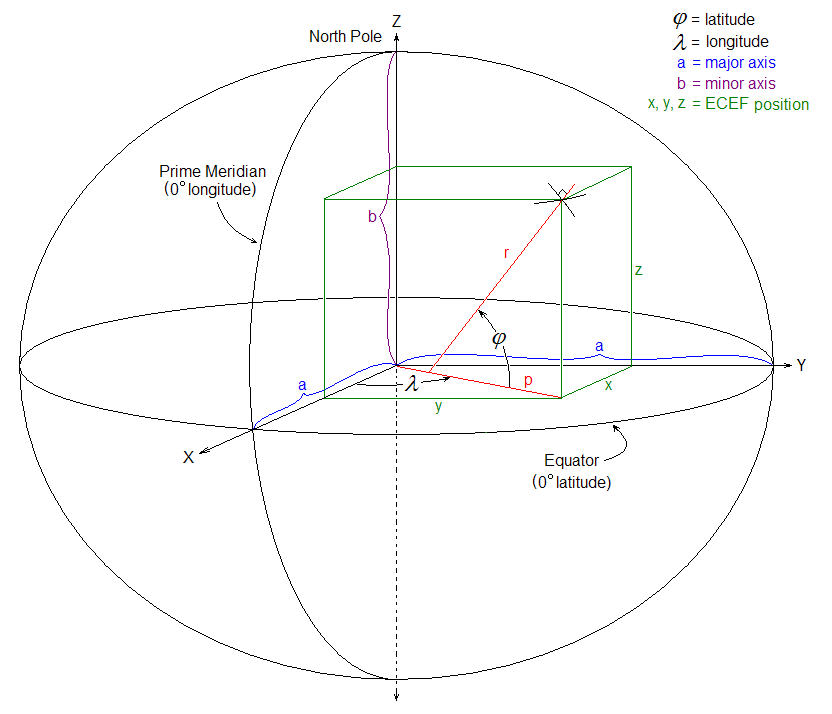
地心地固坐标系（Earth-Centered,Earth-Fixed，简称ECEF）简称地心坐标系，是一种以地心为原点的地固坐标系（也称地球坐标系），是一种笛卡儿坐标系。原点 O (0,0,0)为地球质心，z 轴与地轴平行指向北极点，x 轴指向本初子午线与赤道的交点，y 轴垂直于xOz平面(即东经90度与赤道的交点)构成右手坐标系。

ECEF坐标系有以下参数：

所选椭球中心的原点
Z 轴是北极和南极之间的线，正值向北增加
X轴在赤道平面内，经过原点，从经度180°（负）延伸到本初子午线到经度180°（正）
Y 轴也在赤道平面内，穿过从西经 90°（负）到东经 90°（正）

1.2 LLA坐标

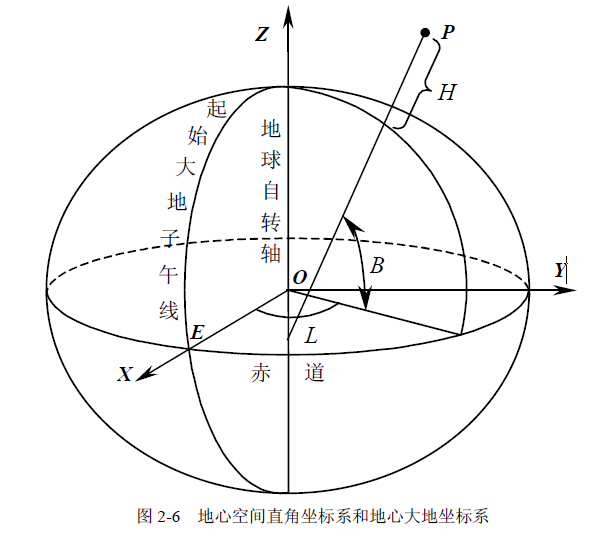
地理坐标系则通过经度(longitude)，纬度(latitude)和高度(altitude)来表示地球的位置，也叫经纬高坐标系(LLA坐标系)。

世界大地测量系统（英语：World Geodetic System, WGS）是一种用于地图学、大地测量学和导航（包括全球定位系统）的大地测量系统标准。WGS包含一套地球的标准经纬坐标系、一个用于计算原始海拔数据的参考椭球体，和一套用以定义海平面高度的引力等势面数据。

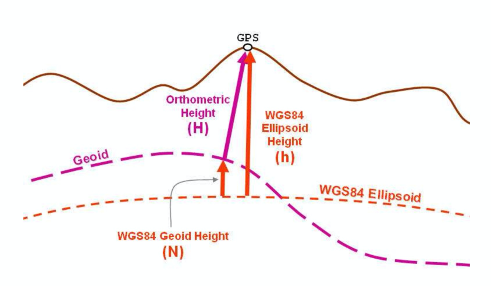
h：从点到基准椭球面的法线距离，即大地高度，外正内负；
H：点到大地水准面的法线距离，海拔高度；
$N_{h}$ ：大地水准面高度，即大地水准面高出基准椭球面的法线距离，它在全球各地区的值可由相关资料查得；

由于地球是个椭球体，可以看出在低纬度地区，0°纬线之间的距离差和1°高纬度地区的纬线距离差是不同的，数值大概都在 111km 左右。1°经线的差异会随着维度不同而不同，可以想象高维度地区越靠近极点，1°经线差异越接近 0km。

参数	WGS-84	CGC200
基准椭球体的长半径a	6378137.0 m	6378137.0 m
基准椭球体的极扁率f	1/298.257223565	1/298.257223563
地球自转角速度We	7.2921151467*1e-5	7.2921151467*1e-5
地球引力和地球质量的乘积GM	3986004.418*1e8	3986004.418*1e8
光速	2.99792458*1e8 m/s	2.99792458*1e8 m/s

1.3 ENU坐标

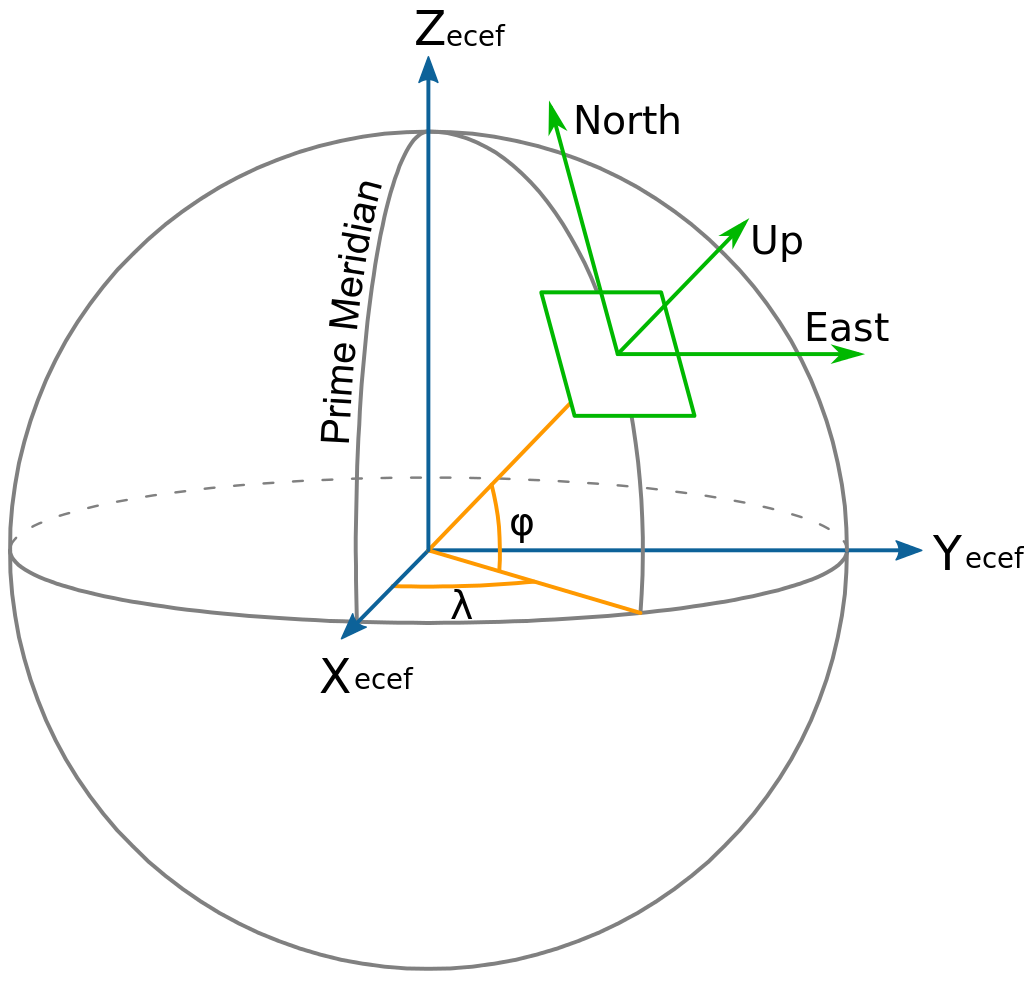
站心地平直角坐标系（East North Up, ENU）是定义在地表正切平面的局部坐标系。如下图所示，它以站心点的纬线方向（指东）为X轴，以站心点的经线方向（指北）为Y轴，以站心点的法线（指上）为Z轴。站心坐标系以用户所在位置P为坐标原点，三个轴分别指向东向，北向和天向，也叫东北天坐标系(ENU坐标系)。

2 坐标转换

2.1 LLA转ECEF

LLA坐标系下的 (lon,lat,alt) 转换为ECEF坐标系下点 (X,Y,Z)。

\[\begin{cases} X &=& (N+alt)\cos(lat)\cos(lon) \\ Y &=& (N+alt)\cos(lat)\sin(lon) \\ Z &=& (N(1-e^{2})+alt)sin(alt) \end{cases}\]

其中e为椭球偏心率，N为基准椭球体的曲率半径。

\[\begin{cases} e^{2} &=& \frac{a^{2}-b^{2}}{a^{2}} \\ N &=& \frac{a}{1- e^{2}\sin^{2}(alt)} \end{cases}\]

由于WGS-84下极扁率 $f=\frac{a−b}{a}$，偏心率 e 和极扁率 f 之间的关系。

\[\begin{aligned} e^{2} = f(2-f) \end{aligned}\]

坐标转换公式也可以为。

\[\begin{aligned} & \begin{cases} X &=& (N+alt)\cos(lat)\cos(lon) \\ Y &=& (N+alt)\cos(lat)\sin(lon) \\ Z &=& (N(1-e^{2})+alt)sin(alt) \end{cases} \\ & N = \frac{a}{\sqrt{1-f(2-f)\sin^{2}(lat)}} \end{aligned}\]

2.2 ECEF转LLA

LLA坐标系下的 (lon,lat,alt) 转换为ECEF坐标系下点 (X,Y,Z)。

\[\begin{aligned} lon &= \arctan(\frac{y}{x}) \\ alt &= \frac{p}{\cos(lat)-N} \\ lat &= \arctan\left[\frac{z}{p}(1-e^{2}\frac{N}{N+alt})^{-1}\right] \\ p &= \sqrt{x^{2}+y^{2}} \end{aligned}\]

一开始 lat 是未知的，可以假设为0，经过几次迭代之后就能收敛。

2.3 ECEF转ENU

用户所在坐标点 P0=(x0,y0,z0)，计算点 P=(x,y,z) 在以点 P0 为坐标原点的enu坐标系位置 (e,n,u) ，这里需要用到 LLA 坐标系的数据，P0的LLA坐标点为 LLA0=(lon0,lat0,alt0)。

\[\left[ \begin{matrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{matrix} \right] = \left[ \begin{matrix} x \\ y \\ z \\ \end{matrix} \right] - \left[ \begin{matrix} x_{0} \\ y_{0} \\ z_{0} \\ \end{matrix} \right]\] \[\left[ \begin{matrix} e \\ n \\ u \\ \end{matrix} \right] = S \cdot \left[ \begin{matrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{matrix} \right] = \left[ \begin{matrix} -\sin(lon_{0}) & \cos(lon_{0}) & 0 \\ -\sin(lon_{0})\cos(lon_{0}) & -\sin(lat_{0})\sin(lon_{0}) & \cos(lat_{0}) \\ \cos(lat_{0})\cos(lon_{0}) & cos(lat_{0})sin(lon_{0}) & \sin(lat_{0}) \\ \end{matrix} \right] \cdot \left[ \begin{matrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{matrix} \right]\]

即坐标变换矩阵。

\[S = \left[ \begin{matrix} -\sin(lon_{0}) & \cos(lon_{0}) & 0 \\ -\sin(lon_{0})\cos(lon_{0}) & -\sin(lat_{0})\sin(lon_{0}) & \cos(lat_{0}) \\ \cos(lat_{0})\cos(lon_{0}) & cos(lat_{0})sin(lon_{0}) & \sin(lat_{0}) \\ \end{matrix} \right]\]

2.4 ENU转ECEF

S为单位正交矩阵

\[S^{-1} = S^{T}\]

反之

\[\left[ \begin{matrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{matrix} \right] = S^{-1} \cdot \left[ \begin{matrix} e \\ n \\ u \\ \end{matrix} \right] = S^{T} \left[ \begin{matrix} e \\ n \\ u \\ \end{matrix} \right]\]

2.5 LLA转ENU

上述可以看到，从 LLA 坐标系转换到 enu 坐标系有较多计算量，在考虑地球偏心率 e 很小的前提下，可以做一定的近似公式计算

\[\left[ \begin{matrix} \Delta e \\ \Delta n \\ \Delta u \\ \end{matrix} \right] = \left[ \begin{matrix} a \cdot \cos(lat) \cdot \Delta{lon} & 0 & 0 \\ 0 & a \cdot \Delta{lat} & 0 \\ 0 & 0 & \Delta{alt} \\ \end{matrix} \right]\]

3 示例代码

3.1 ECEF与LLA

  
#include <iostream>
#include <math.h>

#define M_PI         (3.14159265358979323846)  /* PI */
#define RAD          (57.3248407643312)        /* 1 rad = 57.32° */
#define DEG2RAD(val) (val / RAD)               /* 角度转弧度 */
#define RAD2DEG(val) (val * RAD)               /* 弧度转角度 */
#define WGS84_A      (6378137.0)               /* 基准椭球体的长半径a */
#define WGS84_F      (1 / 298.257223565)       /* 基准椭球体的极扁率f */
#define WGS84_B      ((1 - WGS84_F) * WGS84_A) /* 基准椭球体的长半径b */
#define EPSILON      (0.000000000000001)       /* 误差 */

class Coordinate
{
public:
    Coordinate();
    ~Coordinate();

    /**
     * @brief LLA（WGS84）转ECEF
     * @param lat   纬度，单位度，范围-90~90.
     * @param lon   经度，单位度，范围-180~180.
     * @param alt   高度，单位米.
     * @param x     坐标x，单位米.
     * @param y     坐标y，单位米.
     * @param z     坐标z，单位米.
     */
    static void LLA2ECEF(double lat, double lon, double alt,
        double& x, double& y, double& z);

    /**
     * @brief ECEF转LLA（WGS84）
     * @param x     坐标x，单位米.
     * @param y     坐标y，单位米.
     * @param z     坐标z，单位米.
     * @param lat   纬度，单位度，范围-90~90.
     * @param lon   经度，单位度，范围-180~180.
     * @param alt   高度，单位米.
     */
    static void ECEF2LLA(double x, double y, double z,
        double& lat, double& lon, double& alt);
};

  
#include "Coordinate.h"

Coordinate::Coordinate()
{
}

Coordinate::~Coordinate()
{
}

void Coordinate::LLA2ECEF(double lat, double lon, double alt, double& x, double& y, double& z)
{
    double WGS84_E2 = WGS84_F * (2 - WGS84_F);

    double latRad = DEG2RAD(lat);
    double lonRad = DEG2RAD(lon);
    double N      = WGS84_A / (sqrt(1 - WGS84_E2 * sin(latRad) * sin(latRad)));

    x = (N + alt) * cos(latRad) * cos(lonRad);
    y = (N + alt) * cos(latRad) * sin(lonRad);
    z = (N * (1 - WGS84_E2) + alt) * sin(latRad);
}

void Coordinate::ECEF2LLA(double x, double y, double z, double& lat, double& lon, double& alt)
{
    double WGS84_E = sqrt(WGS84_A * WGS84_A - WGS84_B * WGS84_B) / WGS84_A;
    
    double p       = sqrt(x * x + y * y);
    double N       = 0.0;
    double curLat  = 0.0;
    double calLat  = atan2(z, p);
    for (int i = 0; RAD2DEG(abs(calLat - curLat)) > EPSILON && i < 25; i++)
    {
        curLat = calLat;
        N      = WGS84_A / sqrt(1 - WGS84_E * WGS84_E * sin(curLat) * sin(curLat));
        calLat = atan2(z + N * WGS84_E * WGS84_E * sin(curLat), p);
    }

    lat = RAD2DEG(atan2(y, x));
    lon = RAD2DEG(calLat);
    alt = z / sin(calLat) - N * (1 - WGS84_E * WGS84_E);
}

参考

[1] 参考ECEF与LLA相互转换代码

[2] 地心地固坐标系(ECEF)与站心坐标系(ENU)的转换

[3] wgs_conversions

杂记

坐标转换

本文由作者按照 CC BY 4.0 进行授权

坐标转换

1 坐标分类

1.1 ECEF坐标

1.2 LLA坐标

1.3 ENU坐标

2 坐标转换

2.1 LLA转ECEF

2.2 ECEF转LLA

2.3 ECEF转ENU

2.4 ENU转ECEF

2.5 LLA转ENU

3 示例代码

3.1 ECEF与LLA

参考

热门标签