深度和广度优先遍历

• 深度和广度优先遍历
  • 1 深度优先遍历
    • 1.1 定义
    • 1.2 适用场景
  • 2 广度优先遍历
    • 2.1 定义
    • 2.2 适用场景
  • 3 区别
    • 3.1 图例
    • 3.2 优缺点
  • 4 示例
    • 4.1 DFS
      • 733. 图像渲染
    • 4.2 BFS
      • 994. 腐烂的橘子

该文记录深度和广度优先遍历的主要思想。

深度和广度优先遍历

1 深度优先遍历

1.1 定义

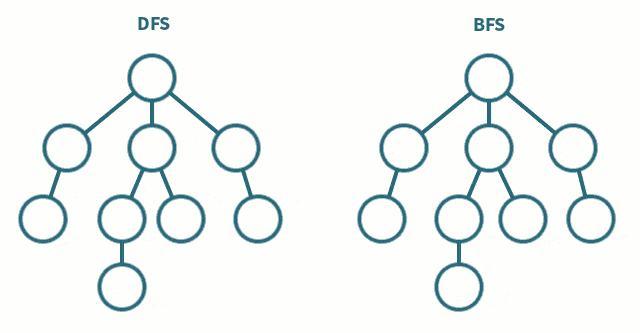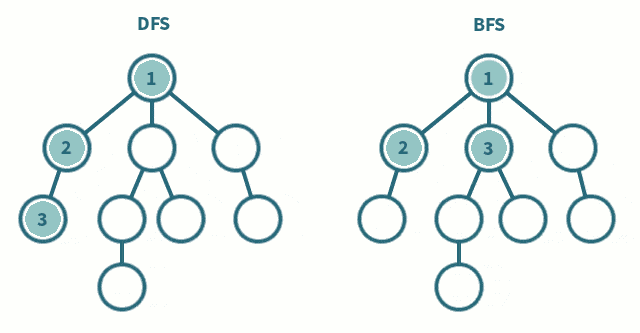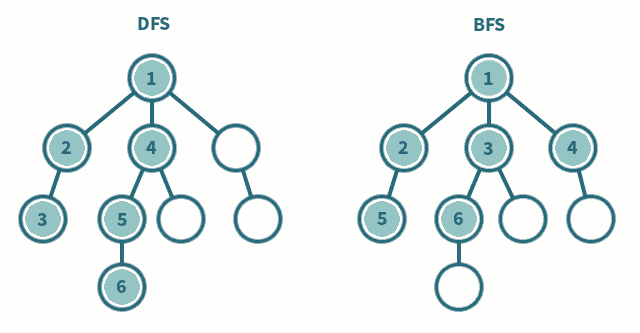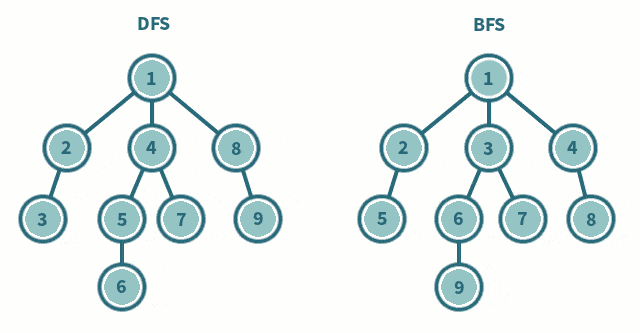
深度优先搜索算法（Depth-First-Search，DFS）是一种用于遍历或搜索 树 或 图 的算法。

这个算法会尽可能深地搜索树的分支。当节点v的所在边e都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

1.2 适用场景

• 多源DFS（求全部方案）

2 广度优先遍历

2.1 定义

广度优先搜索算法（Breadth-First-Search，BFS）是一种 图形 搜索算法。

简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

2.2 适用场景

• 层序遍历
• 最短路径（没有权重）

3 区别

3.1 图例

3.2 优缺点

DFS 可以使用 栈（stack） 和 递归 两种方式实现，为了节省空间一般使用递归实现，这样导致容易堆栈溢出（递归深度不能太深）。

BFS 一般使用 队列（queue） 实现， BFS在搜索过程中需要保存搜索过的状态，而且一般情况需要一个队列来记录，这样空间需求比较大。

4 示例

4.1 DFS

• 递归实现

/**
 * @brief 深度优先遍历
 *  - 把和 image[sr, sc] 颜色一样的且相邻的修改为新颜色
 */
class Solution
{
public:
    const int           dx[4] = {-1, 0, 1, 0}; // 上，右，下，左
    const int           dy[4] = {0, 1, 0, -1};
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor)
    {
        // 栈 保存遍历状态
        stack<pair<int, int>> sta;
        // 初始数据
        if (image[sr][sc] != newColor)
        {
            sta.emplace(sr, sc);
        }

        int oldColor = image[sr][sc];
        while (!sta.empty())
        {
            int x = sta.top().first;
            int y = sta.top().second;
            sta.pop();
            if (oldColor == image[x][y])
            {
                image[x][y] = newColor;
                for (int i = 0; i < 4; i++)
                {
                    int mx = x + dx[i];
                    int my = y + dy[i];
                    if (mx >= 0 && mx < image.size() && my >= 0 && my < image[0].size())
                    {
                        // 更新数据
                        sta.emplace(mx, my);
                    }
                }
            }
        }

        return image;
    }
};

• 栈实现

/**
 * @brief 递归法
 */
class Solution
{
public:
    const int           dx[4] = {-1, 0, 1, 0}; // 上，右，下，左
    const int           dy[4] = {0, 1, 0, -1};
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int newColor)
    {
        if (image[sr][sc] != newColor)
        {
            DFS(image, sr, sc, image[sr][sc], newColor);
        }
        return image;
    }

    void DFS(vector<vector<int>>& image, int sr, int sc, int oldColor, int newColor)
    {
        if (oldColor == image[sr][sc])
        {
            image[sr][sc] = newColor;
            for (int i = 0; i < 4; i++)
            {
                int mx = sr + dx[i];
                int my = sc + dy[i];
                if (mx >= 0 && mx < image.size() && my >= 0 && my < image[0].size())
                {
                    DFS(image, mx, my, oldColor, newColor);
                }
            }
        }
    }
};

733. 图像渲染

4.2 BFS

/**
 * @brief 广度优先遍历，有记录
 */
class Solution
{
public:
    const int dx[4] = {-1, 0, 1, 0}; // 上，右，下，左
    const int dy[4] = {0, 1, 0, -1};
    int       orangesRotting(vector<vector<int>>& grid)
    {
        int                   m = grid.size();
        int                   n = grid[0].size();
        vector<vector<int>>   dist(m, vector<int>(n));
        vector<vector<int>>   seen(m, vector<int>(n));
        queue<pair<int, int>> que;

        // 遍历记录腐烂橘子位置
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (2 == grid[i][j])
                {
                    que.emplace(i, j);
                    seen[i][j] = 1;
                }
            }
        }

        // 广度优先遍历
        while (!que.empty())
        {
            int x = que.front().first;
            int y = que.front().second;
            que.pop();
            for (int i = 0; i < 4; i++)
            {
                int mx = x + dx[i];
                int my = y + dy[i];
                if (mx >= 0 && mx < m && my >= 0 && my < n && 1 == grid[mx][my] && 0 == seen[mx][my])
                {
                    dist[mx][my] = dist[x][y] + 1; // 时间 +1
                    seen[mx][my] = 1;              // 记录遍历过
                    que.emplace(mx, my);           // 添加腐烂橘子位置
                }
            }
        }
        int res = 0;
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (1 == grid[i][j] && 0 == dist[i][j])
                {
                    return -1;
                }
                res = max(dist[i][j], res);
            }
        }
        return res;
    }
};

994. 腐烂的橘子