滑动窗口

• 滑动窗口（Sliding Window）
  • 1 介绍
    • 1.1 定义
    • 1.2 适用范围
    • 1.3 算法思想
  • 2 分类
    • 2.1 固定窗口
    • 2.2 可变窗口
  • 3 示例
    • 3.1 固定窗口
      • 567. 字符串的排列
    • 3.2 可变窗口
      • 3. 无重复字符的最长子串
  • 参考

该文记录滑动窗口的主要思想。

滑动窗口（Sliding Window）

1 介绍

1.1 定义

滑动窗口，就是有一个大小可变的窗口（包含大小固定），左右两端方向一致的向前滑动（右端固定，左端滑动；左端固定，右端滑动）。

可以想象成队列，一端在push元素，另一端在pop元素，如下所示：

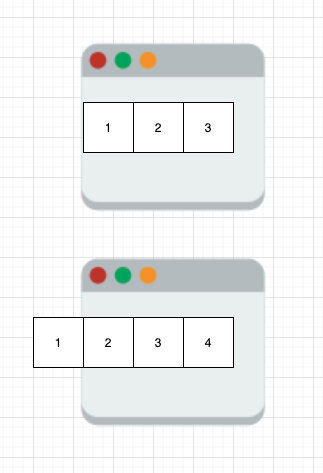
假设有数组[a b c d e f g h]
一个大小为3的滑动窗口在其上滑动，则有:
[a b c]
  [b c d]
    [c d e]
      [d e f]
        [e f g]
          [f g h]

1.2 适用范围

1. 一般是字符串或者列表
2. 一般是要求最值（最大长度，最短长度等等）或者子序列

1.3 算法思想

1. 在序列中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个窗口。
2. 先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的序列符合要求。
3. 此时，停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的序列不再符合要求。同时，每次增加 left 前，都要更新一轮结果。
4. 重复第 2 和第 3 步，直到 right 到达序列的尽头。

思路其实很简单：第 2 步相当于在寻找一个可行解，然后第 3 步在优化这个可行解，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

2 分类

2.1 固定窗口

对于固定窗口，我们只需要固定初始化左右指针 left 和 right，分别表示的窗口的左右顶点，并且保证：

1. left 初始化为 0
2. 初始化 right，使得 right - left + 1 等于窗口大小
3. 同时移动 left 和 right
4. 判断窗口内的连续元素是否满足题目限定的条件
   • 4.1 如果满足，再判断是否需要更新最优解，如果需要则更新最优解
   • 4.2 如果不满足，则继续。

2.2 可变窗口

对于可变窗口，我们同样固定初始化左右指针 left 和 right，分别表示的窗口的左右顶点。后面有所不同，我们需要保证：

1. left 和 right 都初始化为 0
2. right 指针移动一步
3. 判断窗口内的连续元素是否满足题目限定的条件
   • 3.1 如果满足，再判断是否需要更新最优解，如果需要则更新最优解。并尝试通过移动 left 指针缩小窗口大小。循环执行 3.1
   • 3.2 如果不满足，则继续。

形象地来看的话，就是 right 指针不停向右移动，left 指针仅仅在窗口满足条件之后才会移动，起到窗口收缩的效果。

3 示例

3.1 固定窗口

class Solution {
public:
    bool checkInclusion(string s1, string s2)
    {
        int n = s1.length(), m = s2.length();
        if (n > m)
        {
            return false;
        }
        vector<int> cnt1(26), cnt2(26);
        for (int i = 0; i < n; ++i)
        {
            ++cnt1[s1[i] - 'a']; // 取 s1 字符串的 hash 值（只有 s1 的长度窗口）
            ++cnt2[s2[i] - 'a']; // 取 s2 字符串的 hash 值
        }
        if (cnt1 == cnt2)
        {
            return true;
        }
        for (int i = n; i < m; ++i)
        {
            ++cnt2[s2[i] - 'a'];     // 向后移动窗口，后指针后移 加 对应 hash 值
            --cnt2[s2[i - n] - 'a']; // 前指针后移 减 对应 hash 值
            if (cnt1 == cnt2)
            {
                return true;
            }
        }
        return false;
    }
};

567. 字符串的排列

3.2 可变窗口

class Solution
{
public:
    int lengthOfLongestSubstring(string s)
    {
        // 哈希集合，记录每个字符是否出现过
        vector<int> occ(128, -1);
        int         left = -1;
        int         res  = 0;
        for (int right = 0; right < s.size(); ++right)
        {
            left          = max(left, occ[s[right]]);
            res           = max(res, right - left);
            occ[s[right]] = right;
        }
        return res;
    }
};

3. 无重复字符的最长子串

参考

[1] https://github.com/azl397985856/leetcode/blob/master/thinkings/slide-window.md

[2] https://leetcode-cn.com/circle/article/9gcJBk/