文章

算法图解

发表于
作者
34 分钟阅读
算法图解

该文记录《算法图解》主要内容。

算法图解

1 算法简介

1.2 二分查找

仅当列表是有序的时候，二分查找才管用

1.2.2 运行时间

最多需要猜测的次数与列表长度相同，这被称为线性时间（linear time）。

二分查找的运行时间为对数时间（或log时间）

1.3 大O表示法

大O表示法指的并非以秒为单位的速度。大O表示法让你能够比较操作数，它指出了算法运行时间的增速。

1.3.4 一些常见的大O运行时间

  • O(log n)，也叫对数时间，这样的算法包括二分查找。
  • O(n)，也叫线性时间，这样的算法包括简单查找。
  • O(n * log n)，这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
  • O($n^2$)，这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。
  • O(n!)，这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。

1.4 小结

  1. 二分查找的速度比简单查找快得多。
  2. O(log n)比O(n)快。需要搜索的元素越多，前者比后者就快得越多。
  3. 算法运行时间并不以秒为单位。
  4. 算法运行时间是从其增速的角度度量的。
  5. 算法运行时间用大O表示法表示。

2 选择排序

2.2 数组和链表

2.2.1 链表

链表中的元素可存储在内存的任何地方。链表的每个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串在一起。

缺点：读取必须依次顺序遍历。

2.2.2 数组

数组与知道其中每个元素的地址。

缺点：插入和删除需要移动后面元素。

2.2.3 术语

  • 数组的元素带编号，编号从0而不是1开始。

  • 元素的位置称为索引。

数组链表和链表数组。

2.4 小结

  1. 计算机内存犹如一大堆抽屉。
  2. 需要存储多个元素时，可使用数组或链表。
  3. 数组的元素都在一起。
  4. 链表的元素是分开的，其中每个元素都存储了下一个元素的地址。
  5. 数组的读取速度很快。
  6. 链表的插入和删除速度很快。
  7. 在同一个数组中，所有元素的类型都必须相同（都为int、double等）

3 递归

3.1 递归

递归——函数调用自己。

Leigh Caldwell 在 Stack Overflow 上说的一句话：“如果使用循环，程序的性能可能更高；如果使用递归，程序可能更容易理解。如何选择要看什么对你来说更重要。”

3.2 基线条件和递归条件

每个递归函数都有两部分：基线条件（base case）和递归条件（recursive case）

递归条件指的是函数调用自己，而基线条件则指的是函数不再调用自己，从而避免形成无限循环。

3.3 栈

压入（插入）和弹出（删除并读取），这种数据结构称为栈。

缺点：存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。在这种情况下，你有两种选择。

  • 重新编写代码，转而使用循环。

  • 使用尾递归。这

3.4 小结

  1. 递归指的是调用自己的函数。
  2. 每个递归函数都有两个条件：基线条件和递归条件。
  3. 栈有两种操作：压入和弹出。
  4. 所有函数调用都进入调用栈。
  5. 调用栈可能很长，这将占用大量的内存。

4 快速排序

分而治之（divide and conquer，D&C）——一种著名的递归式问题解决方法。

4.1 分而治之

使用D&C解决问题的过程包括两个步骤。

(1) 找出基线条件，这种条件必须尽可能简单。

(2) 不断将问题分解（或者说缩小规模），直到符合基线条件。

4.2 快速排序

(1) 选择基准值。

(2) 将数组分成两个子数组：小于基准值的元素和大于基准值的元素。

(3) 对这两个子数组进行快速排序（重复上述步骤）。

4.4 小结

  1. D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元 素的数组。
  2. 实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为O(n log n)。
  3. 大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。
  4. 比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O(log n)的速度比O(n) 快得多。

5 散列表

5.1 散列函数

散列表可能是最有用的，也被称为散列映射、映射、字典和关联数组。散列表由键和值组成。

5.2 应用案例

5.2.1 将散列表用于查找

  • 电话簿
  • DNS解析（DNS resolution）

5.2.2 防止重复

  • 投票

5.2.3 将散列表用于缓存

  • 网站缓存

5.2.4 小结

散列表适合用于：

  1. 模拟映射关系；
  2. 防止重复；
  3. 缓存/记住数据，以免服务器再通过处理来生成它们。

5.3 冲突

冲突（collision）：给两个键分配的位置相同。

5.4 性能

避免冲突，需要有：

  • 较低的填装因子；
  • 良好的散列函数。

5.4.1 填装因子

填装因子 = 散列表包含的元素数 / 位置总数

一旦填装因子开始增大，你就需要在散列表中添加位置，这被称为调整长度（resizing）。通常将数组增长一倍。

5.4.2 良好的散列函数

可将SHA函数用作散列函数。

5.5 小结

你几乎根本不用自己去实现散列表，因为你使用的编程语言提供了散列表实现。假定能够获得平均情况下的性能：常量时间。

  1. 你可以结合散列函数和数组来创建散列表。
  2. 冲突很糟糕，你应使用可以最大限度减少冲突的散列函数。
  3. 散列表的查找、插入和删除速度都非常快。
  4. 散列表适合用于模拟映射关系。
  5. 一旦填装因子超过0.7，就该调整散列表的长度。
  6. 散列表可用于缓存数据（例如，在Web服务器上）。
  7. 散列表非常适合用于防止重复。

6 广度优先搜索

广度优先搜索（breadth-first search，BFS）。广度优先搜索让你能够找出两样东西之间的最短距离。

6.1 图简介

解决最短路径问题的算法被称为广度优先搜索。

6.2 图是什么

图模拟一组连接。图由节点和边组成。一个节点可能与众多节点直接相连，这些节点被称为邻居。

6.3 广度优先搜索

6.3.1 查找最短路径

在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查二度关系。只有按添加顺序查找时，才能实现这样的目的。

6.3.2 队列

队列只支持两种操作：入队和出队。

队列是一种先进先出（First In First Out，FIFO）的数据结构，而栈是一种后进先出（Last In First Out，LIFO）的数据结构。

6.4 实现图

图由多个节点组成。

有向图（directed graph），其中的关系是单向的

无向图（undirected graph）没有箭头，直接相连的节点互为邻居。

6.5 实现算法

6.6 小结

  1. 广度优先搜索指出是否有从A到B的路径。
  2. 如果有，广度优先搜索将找出最短路径。
  3. 面临类似于寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来解决问题。
  4. 有向图中的边为箭头，箭头的方向指定了关系的方向。
  5. 无向图中的边不带箭头，其中的关系是双向的。
  6. 队列是先进先出（FIFO）的。
  7. 栈是后进先出（LIFO）的。
  8. 必须顺序搜索列表，所以搜索列表必须是队列。
  9. 对于检查过的人，务必不要再去检查，否则可能导致无限循环。

7 狄克斯特拉算法

7.1 使用狄克斯特拉算法

狄克斯特拉算法（Dijkstra’s algorithm）。

image-20220811235719643

狄克斯特拉算法包含4个步骤。

(1) 找出最便宜的节点，即可在最短时间内前往的节点。

(2) 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。

(3) 重复这个过程，直到对图中的每个节点都这样做了。

(4) 计算最终路径。

7.2 术语

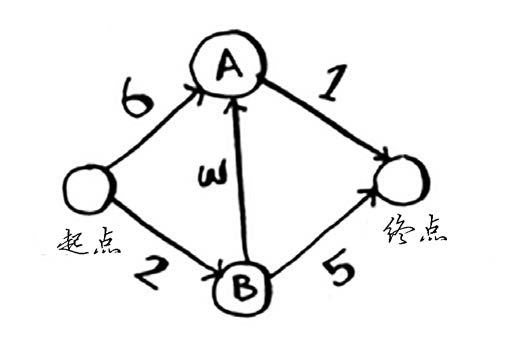
狄克斯特拉算法用于每条边都有关联数字的图，这些数字称为权重（weight）。

带权重的图称为加权图（weighted graph），不带权重的图称为非加权图（unweighted graph）。

要计算非加权图中的最短路径，可使用广度优先搜索。要计算加权图中的最短路径，可使用狄克斯特拉算法。图还可能有环。

在无向图中，每条边都是一个环。狄克斯特拉算法只适用于有向无环图（directed acyclic graph，DAG）。

7.3 换钢琴

7.4 负权边

不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼-福德算法（Bellman-Ford algorithm）。

7.5 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

#include <iostream>
#include <queue>
#include <utility>
#include <vector>
using namespace std;

#define INF 0x3f3f3f3f

// iPair ==> Integer Pair（整数对）
typedef pair<int, int> iPair;

// 加边
void addEdge(vector<pair<int, int>> adj[], int u, int v, int wt)
{
    adj[u].push_back(make_pair(v, wt));
    adj[v].push_back(make_pair(u, wt));
}

// 计算最短路
void shortestPath(vector<pair<int, int>> adj[], int V, int src)
{
    // 关于stl中的优先队列如何实现，参考下方网址：
    // http://geeksquiz.com/implement-min-heap-using-stl/
    priority_queue<iPair, vector<iPair>, greater<iPair>> pq;

    // 距离置为正无穷大
    vector<int>  dist(V, INF);
    vector<bool> visited(V, false);

    // 插入源点，距离为0
    pq.push(make_pair(0, src));
    dist[src] = 0;

    /* 循环直到优先队列为空 */
    while (!pq.empty())
    {
        // 每次从优先队列中取出顶点事实上是这一轮最短路径权值确定的点
        int u = pq.top().second;
        pq.pop();
        if (visited[u])
        {
            continue;
        }
        visited[u] = true;
        // 遍历所有边
        for (auto x : adj[u])
        {
            // 得到顶点边号以及边权
            int v      = x.first;
            int weight = x.second;

            //可以松弛
            if (dist[v] > dist[u] + weight)
            {
                // 松弛
                dist[v] = dist[u] + weight;
                pq.push(make_pair(dist[v], v));
            }
        }
    }

    // 打印最短路
    printf("Vertex Distance from Source\n");
    for (int i = 0; i < V; ++i)
        printf("%d \t\t %d\n", i, dist[i]);
}
int main()
{
    int           V = 9;
    vector<iPair> adj[V];
    addEdge(adj, 0, 1, 4);
    addEdge(adj, 0, 7, 8);
    addEdge(adj, 1, 2, 8);
    addEdge(adj, 1, 7, 11);
    addEdge(adj, 2, 3, 7);
    addEdge(adj, 2, 8, 2);
    addEdge(adj, 2, 5, 4);
    addEdge(adj, 3, 4, 9);
    addEdge(adj, 3, 5, 14);
    addEdge(adj, 4, 5, 10);
    addEdge(adj, 5, 6, 2);
    addEdge(adj, 6, 7, 1);
    addEdge(adj, 6, 8, 6);
    addEdge(adj, 7, 8, 7);

    shortestPath(adj, V, 0);

    return 0;
}

7.6 小结

  1. 广度优先搜索用于在非加权图中查找最短路径。
  2. 狄克斯特拉算法用于在加权图中查找最短路径。
  3. 仅当权重为正时狄克斯特拉算法才管用。
  4. 如果图中包含负权边，请使用贝尔曼-福德算法。

8 贪婪算法

8.1 教室调度问题

贪婪算法很简单：每步都采取最优的做法。

每步都选择局部最优解，最终得到的就是全局最优解。

8.2 背包问题

贪婪策略显然不能获得最优解，但非常接近。

8.3 集合覆盖问题

近似算法

8.4 NP 完全问题

8.4.1 旅行商问题详解

随便选择出发城市，然后每次选择要去的下一个城市时，都选择还没去的最近的城市。

8.4.2 如何识别 NP 完全问题

  • 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
  • 涉及“所有组合”的问题通常是NP完全问题。
  • 不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
  • 如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
  • 如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
  • 如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。

8.5 小结

  1. 贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
  2. 对于NP完全问题，还没有找到快速解决方案。
  3. 面临NP完全问题时，最佳的做法是使用近似算法。
  4. 贪婪算法易于实现、运行速度快，是不错的近似算法。

9 动态规划

9.1 背包问题

9.1.1 简单算法

尝试各种可能的商品组合，并找出价值最高的组合。$O(2^n)$

9.1.2 动态规划

image-20220821173633686

9.2 背包问题 FAQ

9.3 最长公共子串

动态规划问题启示

  • 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
  • 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。

下面是一些通用的小贴士。

  • 每种动态规划解决方案都涉及网格。
  • 单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。
  • 每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴。

9.3.1 绘制网格

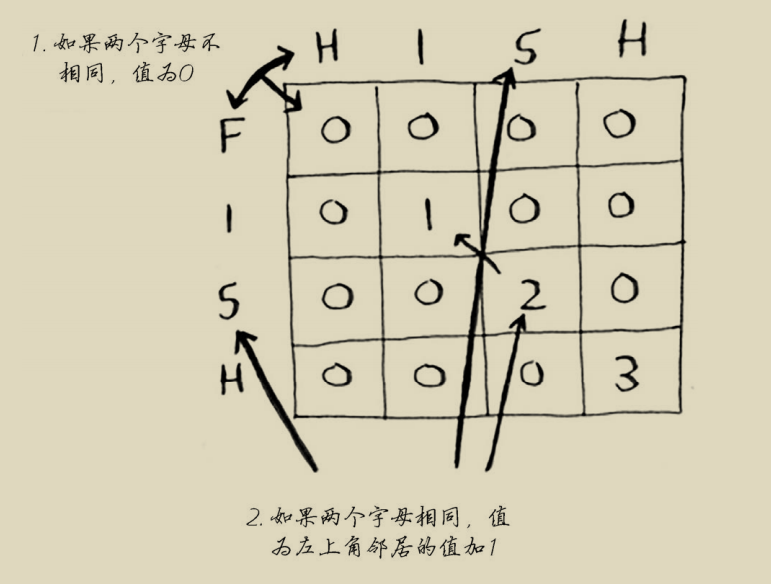
9.3.2 填充网格

9.3.3 揭晓答案

image-20220821174711339

但对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中。

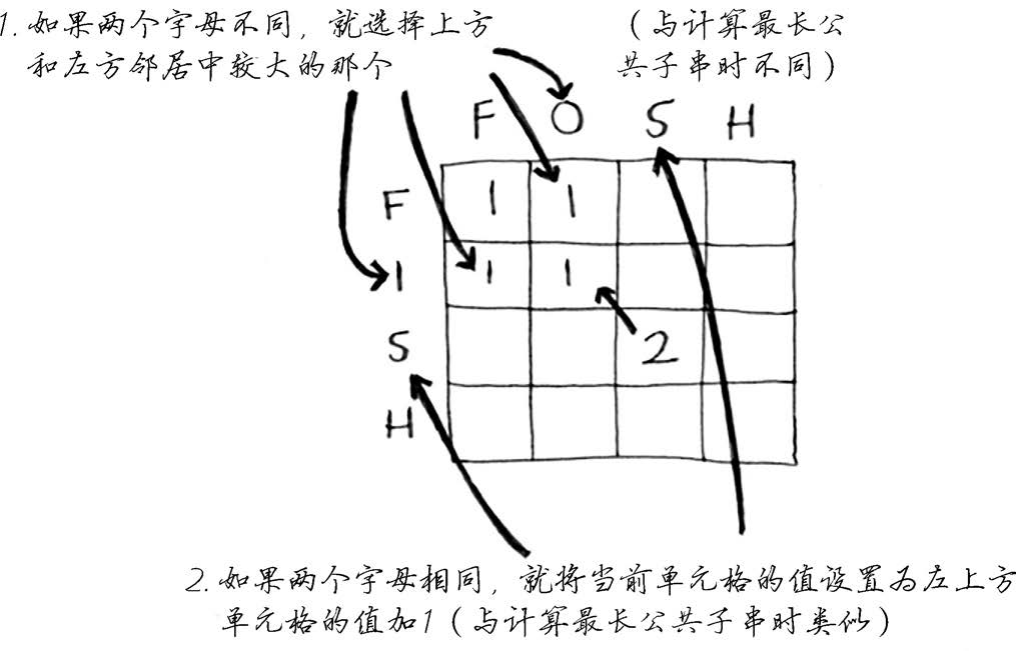
9.3.4 最长公共子序列

最长公共子序列：两个单词中都有的序列包含的字母数。

9.3.5 最长公共子序列之解决方案

image-20220821175012756

9.4 小结

  1. 需要在给定约束条件下优化某种指标时，动态规划很有用。
  2. 问题可分解为离散子问题时，可使用动态规划来解决。
  3. 每种动态规划解决方案都涉及网格。
  4. 单元格中的值通常就是你要优化的值。
  5. 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
  6. 没有放之四海皆准的计算动态规划解决方案的公式。

10 K最近邻算法

10.1 橙子还是柚子

K最近邻（k-nearest neighbours，KNN）算法：如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。

10.2 创建推荐系统

10.2.1 特征抽取

10.2.2 回归

求K最近邻的平均值，这就是回归（regression）。使用KNN来做两项基本工作——分类和回归：

  • 分类就是编组；
  • 回归就是预测结果（如一个数字）。

余弦相似度（cosine similarity）。余弦相似度不计算两个矢量的距离，而比较它们的角度。

10.2.3 挑选合适的特征

10.3 机器学习简介

10.3.1 OCR

OCR 指的是光学字符识别（optical character recognition），这意味着你可拍摄印刷页面的照片，计算机将自动识别出其中的文字。Google 使用 OCR 来实现图书数字化。

OCR 算法提取线段、点和曲线等特征。

OCR 的第一步是查看大量的数字图像并提取特征，这被称为训练（training）。

10.3.2 创建垃圾邮件过滤器

垃圾邮件过滤器使用一种简单算法——朴素贝叶斯分类器（Naive Bayes classifier）。

10.3.3 预测股票市场

未来很难预测，由于涉及的变数太多，这几乎是不可能完成的任务。

10.4 小结

  1. KNN 用于分类和回归，需要考虑最近的邻居。
  2. 分类就是编组。
  3. 回归就是预测结果（如数字）。
  4. 特征抽取意味着将物品（如水果或用户）转换为一系列可比较的数字。
  5. 能否挑选合适的特征事关 KNN 算法的成败。

11 接下来如何做

11.1 树

二叉查找树（binary search tree）。

二叉查找树中查找节点时，平均运行时间为 $O(log{n})$，但在最糟的情况下所需时间为 $O(n)$；

二叉查找树也存在一些缺点，例如，不能随机访问。

如果你对数据库或高级数据结构感兴趣，请研究如下数据结构：B树，红黑树，堆，伸展树。

11.2 反向索引

一个散列表，将单词映射到包含它的页面。这种数据结构被称为反向索引（inverted index），常用于创建搜索引擎。

11.3 傅里叶变换

11.4 并行算法

  • 并行性管理开销。合并也是需要时间的。
  • 负载均衡。子任务快慢不同。

11.5 MapReduce

有一种特殊的并行算法正越来越流行，它就是分布式算法。

在并行算法只需两到四个内核时，完全可以在笔记本电脑上运行它，但如果需要数百个内核呢？在这种情况下，可让算法在多台计算机上运行。MapReduce 是一种流行的分布式算法，你可通过流行的开源工具 Apache Hadoop 来使用它。

11.5.1 分布式算法为何很有用

分布式算法非常适合用于在短时间内完成海量工作，其中的 MapReduce 基于两个简单的理念：映射（map）函数和归并（reduce）函数。

11.5.2 映射函数

映射函数很简单，它接受一个数组，并对其中的每个元素执行同样的处理。

11.5.3 归并函数

归并函数理念是将很多项归并为一项。映射是将一个数组转换为另一个数组。

11.6 布隆过滤器和 HyperLogLog

假设你在 Google 负责搜集网页，但只想搜集新出现的网页，因此需要判断网页是否搜集过。

只是 Google 需要建立数万亿个网页的索引，因此这个散列表非常大，需要占用大量的存储空间。

11.6.1 布隆过滤器

布隆过滤器是一种概率型数据结构，它提供的答案有可能不对，但很可能是正确的。

  • 可能出现错报的情况，即 Google 可能指出“这个网站已搜集”，但实际上并没有搜集。
  • 不可能出现漏报的情况，即如果布隆过滤器说“这个网站未搜集”，就肯定未搜集。

11.6.2 HyperLogLog

HyperLogLog 近似地计算集合中不同的元素数，与布隆过滤器一样，它不能给出准确的答案，但也八九不离十，而占用的内存空间却少得多。

面临海量数据且只要求答案八九不离十时，可考虑使用概率型算法！

11.7 SHA 算法

11.7.1 比较文件

另一种散列函数是安全散列算法（secure hash algorithm，SHA）函数。给定一个字符串，SHA 返回其散列值。

SHA 是一个散列函数，它生成一个散列值——一个较短的字符串。

11.7.2 检查密码

SHA 被广泛用于计算密码的散列值。这种散列算法是单向的。

11.8 局部敏感的散列算法

Simhash 生成的散列值也只存在细微的差别。这让你能够通过比较散列值来判断两个字符串的相似程度，这很有用！

11.9 Diffie-Hellman 密钥交换

Diffie-Hellman 算法解决了如下两个问题。

  • 双方无需知道加密算法。他们不必会面协商要使用的加密算法。
  • 要破解加密的消息比登天还难。

Diffie-Hellman 使用两个密钥：公钥和私钥。

Diffie-Hellman 算法及其替代者 RSA 依然被广泛使用。如果你对加密感兴趣，先着手研究 Diffie-Hellman 算法是不错的选择：它既优雅又不难理解。

11.10 线性规划

Book
Book
本文由作者按照 CC BY 4.0 进行授权