递归和迭代

• 递归和迭代
  • 1 递归
    • 1.1 定义
  • 2 迭代
    • 2.1 定义
  • 3 区别
    • 3.1 关系
    • 3.2 优缺点
  • 4 示例
    • 4.1 递归
      • 79. 单词搜索
    • 4.2 迭代
      • 509. 斐波那契数

该文记录递归和迭代的主要思想。

递归和迭代

1 递归

1.1 定义

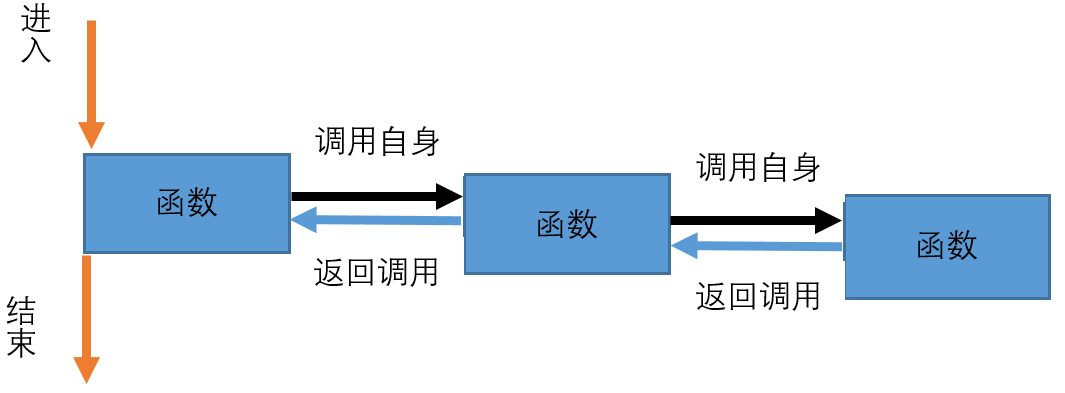
递归（recursion）：重复调用函数自身实现循环称为递归。

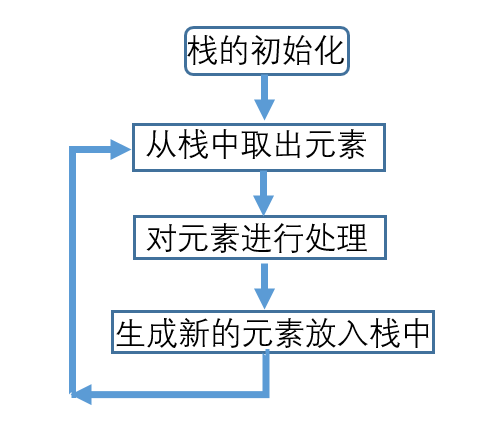
递归实际上不断地深层调用函数，直到函数有返回才会逐层的返回，递归是用栈机制实现的，每深入一层，都要占去一块栈数据区域，因此，递归涉及到运行时的堆栈开销（参数必须压入堆栈保存，直到该层函数调用返回为止），所以有可能导致堆栈溢出的错误；但是递归编程所体现的思想正是人们追求简洁、将问题交给计算机，以及将大问题分解为相同小问题从而解决大问题的动机。

2 迭代

2.1 定义

迭代（iteration）：利用变量的原值推出新值称为迭代，或着说迭代是函数内某段代码实现循环。

迭代大部分时候需要人为的对问题进行剖析，分析问题的规律所在，将问题转变为一次次的迭代来逼近答案。迭代不像递归那样对堆栈有一定的要求，另外一旦问题剖析完毕，就可以很容易的通过循环加以实现。

3 区别

3.1 关系

• 两者关系：所有的迭代可以转换为递归，但递归不一定可以转换成迭代。
• 注意：能用迭代不用递归（因为递归不断调用函数，浪费空间，容易造成堆栈溢出）

3.2 优缺点

	定义	优点	缺点
递归	重复调用函数自身实现循环	1. 用有限的循环语句实现无限集合； 2. 代码易读； 3. 大问题转化成小问题，减少了代码量。	1. 递归不断调用函数，浪费空间 2. 容易造成堆栈溢出
迭代	利用变量的原值推出新值；函数内某段代码实现循环。	1. 效率高，运行时间只随循环的增加而增加； 2. 无额外开销。	1. 代码难理解； 2. 代码不如递归代码简洁； 3. 编写复杂问题时，代码逻辑不易想出

4 示例

4.1 递归

79. 单词搜索

/**
 * @brief 递归
 *  - 找到对应的字符，然后上下左右进行判断，符合条件递归调用，
 *  - 当不满足条件就进行回溯。
 */
class Solution
{
public:
    const int dx[4] = {-1, 0, 1, 0}; // 上，右，下，左
    const int dy[4] = {0, 1, 0, -1};

    /**
     * @brief 递归（条件判断，记录遍历路径）
     * 
     * @param board    二维字符网格
     * @param word     字符串单词
     * @param index    字符串下标
     * @param x        二维坐标，行
     * @param y        二维坐标，列
     */
    bool backtrack(vector<vector<char>>& board, string& word, int index, int x, int y)
    {
        if (index == word.size())
        {
            return true;
        }

        for (int i = 0; i < 4; i++)
        {
            int mx = x + dx[i];
            int my = y + dy[i];
            if (mx >= 0 && mx < board.size() && my >= 0 && my < board[0].size() && board[mx][my] == word[index])
            {
                // 记录已经遍历路径，回溯时复原
                char c      = board[x][y];
                board[x][y] = ' ';
                if (backtrack(board, word, index + 1, mx, my))
                {
                    return true;
                }
                board[x][y] = c;
            }
        }
        return false;
    }

    bool exist(vector<vector<char>>& board, string word)
    {
        for (size_t i = 0; i < board.size(); i++)
        {
            for (size_t j = 0; j < board[0].size(); j++)
            {
                if (board[i][j] == word[0])
                {
                    if (backtrack(board, word, 1, i, j))
                        return true;
                }
            }
        }
        return false;
    }
};

4.2 迭代

509. 斐波那契数

/**
 * @brief 迭代
 *  - 计算得到新结果，并将原始数据进行迭代更新
 */
class Solution
{
public:
    int fib(int n)
    {
        if (n == 0)
        {
            return 0;
        }
        if (n == 1)
        {
            return 1;
        }

        int pre = 0, next = 1, res = 0;
        while (n-- > 1)
        {
            res  = pre + next;
            pre  = next;
            next = res;
        }
        return res;
    }
};